CAVEON SECURITY INSIGHTS BLOG
The World's Only Test Security Blog
Pull up a chair among Caveon's experts in psychometrics, psychology, data science, test security, law, education, and oh-so-many other fields and join in the conversation about all things test security.
Are Identical Exam Answers Proof of Cheating on a Test?
Posted by Dennis Maynes
updated over a week ago
Introduction
Test-taking data uncover many forms of cheating and test fraud. From wrong-to-right answer changes, to inconsistent test-taking behavior, to unusual response times—data forensics analyses are one of the most effective tools a testing program can utilize to protect the validity of their exam scores.
When cheating does happen, how can you prove that cheating actually occurred? Statistical evidence is a great place to start. And when it comes to supporting an allegation of cheating on tests, there is rarely better statistical evidence than having two (or more) tests with identical sets of responses.
Example Instances of Answer Similarity
Having a great interest in this topic, I have read carefully many abstracts, including those of Rice University Honor Council meetings, where these types of allegations are taken very seriously.
In several instances of alleged academic fraud, the Honor Council of Rice University has met and found the evidence of identical solutions and identical answers to be compelling. For example, below are the Council minutes for two separate cases.
Case 1: Honor Code Violation Not Present
The minutes for this case read:
Witness 1, the professor for the class, stated that he believed the similarities between the True / False answers and the essay answers given by Student A and Student B to be strikingly similar. He… presented a statistical analysis of the probability of this occurring in certain situations.
In the above case, despite having a probability analysis, the Honor Council did not find that the honor code had been violated (i.e., cheating was not found). In another instance, however, the Honor Council came to a different conclusion—outlined in Case 2 below.
Case 2: Honor Code Violation Present
The minutes for this case read:
Some members felt that the identical answers on some portions of the exam were beyond coincidence or having similar notes or studying together. Members were suspicious of the fact that these similarities would arise after the students used different sources of information when answering the questions... Some members were not convinced by the explanations.
Despite denials of cheating in the above situation, both students were found in violation of the Honor Code.
So why is it that, in some cases, cheating is considered to be the cause of answer similarity, but in other cases, it is not? The short answer is: "It is up to the program to decide. In many situations, you can obtain very strong and reliable evidence leading you to conclude that cheating occurred—and the conclusion would be right, nearly always."
But how do you make the decision on whether cheating actually occurred?
How to Discern Whether Answer Similarities = Cheating
The "Beyond a Reasonable Doubt" Standard
From the above two abstracts, it is evident that testing programs can attempt to find plausible explanations for identical answers and excessive similarities between test questions. It is also evident that testing programs can act (and have the right to act) without definitive proof. As an example of the degree of “proof” or evidence that may be required to take action in a case of suspected cheating, consider this statement from the University of Western Ontario:
It is particularly important to understand that the conclusion that a student committed a scholastic offense does not have to be supported by evidence beyond a reasonable doubt. In an exam writing situation, that means that a decision-maker may conclude that cheating took place, even if it is possible that two people got some identical answers by chance.
As defined in the above statement, the observation that two tests have identical answers is very reliable evidence on its own. The observation in this scenario is (1) factual, (2) objective, (3) credible, and (4) defensible. However, the observation must have one additional attribute before assuming that cheating likely occurred: the evidence must be strong.
The "Strong Evidence" Principle
In any given scenario, when determining whether identical answers are proof of cheating, you must observe the facts and have strong evidence that supports your decision. Ensure your observation of each incident is:
- Factual
- Objective
- Credible
- Defensible, and
- Supported by Strong Evidence
In order to evaluate the strength of the evidence in identical answers, you should include the probability of the observed responses. The probability for the observed item responses can be estimated using item response theory. You can compute this probability by multiplying all the probabilities together of the selected responses (we assume the selected responses are conditionally independent) and then normalizing the product by the marginal probability of the observed score.
With that said, formulas for computing exact probabilities are difficult to derive and program. Because of this, most practitioners who encounter these situations rely upon judgment and intuition—the same way the Rice Honor Council did in Cases 1 & 2 outlined above.
Sample Probabilities
Below is a table of sampled probabilities for an 18-item test. The probabilities are calculated knowing the score that was obtained on the test. So, if we know a person answered all 18 items correctly, the probability that another person who answered all 18 items correctly would match is equal to one. If the answer was correct, it is highlighted in gold in the table.
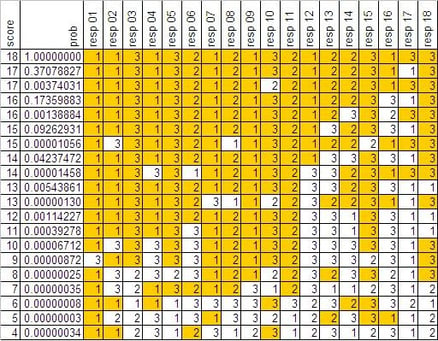
Even though I routinely evaluate these types of probabilities, I have been surprised by some instances of identical response data. For example, the probability of an identical test when all items are answered correctly is 1 (as in the first row of the table). However, the probability of an identical test when all but one or two questions are answered correctly may be as high as .10 or .25 (see the second and fourth rows of the table). On the other hand, if several questions are answered incorrectly, the probability of an identical test may be one in 100 million or even smaller. The wide variation in these probabilities is a function of the number of correctly answered test questions and the selected responses.
If the probabilities of some test response patterns are sufficiently high (for example, if the test is easy or the examinees are very proficient) and if we have a large enough group, we might expect to see many identical tests. Probability computations for the number of observed identical tests can be very difficult. This is an instance of the “birthday problem” with unequal probabilities. (The birthday problem concerns the probability that, in a set of n randomly chosen people, some pair of them will have the same birthday—see this article for more information). This is important information to keep in mind.
Conclusion
At the beginning of this discussion, it appeared that we had a relatively straightforward and simple problem. It often occurs with statistics that many apparently simple problems become very complex, very quickly. The analysis of identical answers for two exams is one of those more complex problems.
The answer to the question "Are identical exam answers proof of cheating on a test?" is:
We cannot prove that cheating occurred when we have identical answers for two test instances. However, in many situations, we can obtain very strong and reliable evidence leading us to conclude that cheating occurred—and the conclusion would be right, nearly always.
When determining whether identical answers are proof of cheating, always observe the facts and provide statistical evidence that supports your decision. And while the observation that two tests have identical answers is very reliable evidence on its own, you should always use your best judgment and hold observations that are factual, objective, credible, defensible, and supported by strong statistical evidence (such as the probability of the observed responses).
Dennis Maynes
View all articlesAbout Caveon
For more than 18 years, Caveon Test Security has driven the discussion and practice of exam security in the testing industry. Today, as the recognized leader in the field, we have expanded our offerings to encompass innovative solutions and technologies that provide comprehensive protection: Solutions designed to detect, deter, and even prevent test fraud.
Posts by Topic
- Test Security Basics (34)
- Detection Measures (29)
- K-12 Education (27)
- Online Exams (21)
- Test Security Plan (21)
- Higher Education (20)
- Prevention Measures (20)
- Test Security Consulting (20)
- Certification (19)
- Exam Development (19)
- Deterrence Measures (15)
- Medical Licensure (15)
- Web Monitoring (12)
- DOMC™ (11)
- Data Forensics (11)
- Investigating Security Incidents (11)
- Test Security Stories (9)
- Security Incident Response Plan (8)
- Monitoring Test Administration (7)
- SmartItem™ (7)
- Automated Item Generation (AIG) (6)
- Braindumps (6)
- Proctoring (4)
- DMCA Letters (2)
Recent Posts
SUBSCRIBE TO OUR NEWSLETTER
Get expert knowledge delivered straight to your inbox, including exclusive access to industry publications and Caveon's subscriber-only resource, The Lockbox.

